Introduction to Thermodynamics
Some useful constants in thermodynamics:
- 1 eV = 9.6522E4 J/mol
- k, Boltzmann's constant = 1.38E-23 J/K
- volume: 1 cm3 = 0.1 kJ/kbar = 0.1 J/bar
- mole: 1 mole of a substance contains Avogadro's number (N = 6.02E23) of molecules. Abbreviated as 'mol'.
- atomic weights are based around the definition that 12C is exactly 12 g/mol
- R gas constant = Nk = 8.314 J mol-1 K-1
Units of Temperature: Degrees Celsius and Kelvin
The Celsius scale is based on defining 0 °C as the freezing point of water and 100°C as the boiling point.
The Kelvin scale is based on defining 0 K, "absolute zero," as the
temperature at zero pressure where the volumes of all gases is
zero--this turns out to be -273.15 °C. This definition means that the
freezing temperature of water is 273.15 K. All thermodynamic
calculations are done in Kelvin!
kilo and kelvin: write k for 1000's and K for kelvin. Never write °K.
Units of Energy: Joules and Calories
Joules and calories and kilocalories: A calorie is defined as the
amount of energy required to raise the temperature of 1 g of water from
14.5 to 15.5°C at 1 atm.
4.184 J = 1 cal; all food 'calories' are really kcal.
Many times it is easiest to solve equations or problems by
conducting "dimensional analysis," which just means using the same
units throughout an equation, seeing that both sides of an equation
contain balanced units, and that the answer is cast in terms of units
that you want. As an example, consider the difference between
temperature (units of K) and heat (units of J). Two bodies may have the
same temperature, but contain different amounts of heat; likewise, two
bodies may contain the same heat, but be at different temperatures. The
quantity that links these two variables must have units of J/K or K/J.
In fact, the heat capacity C describes the amount of heat dQ involved
in changing one mole of a substance by a given temperature increment
dT:
The heat capacity C is then
and must have units of J K-1 mol-1. (The specific heat is essentially the same number, but is expressed per gram rather than per mole.)
Don't forget significant digits. 1*2=2; 1.1*2=2; 1.1*2.0=2.2; 1.0*2.0=2.0
Why Thermodynamics?
Think about some everyday experiences you have with chemical reactions.
Your ability to melt and refreeze ice shows you that H2O
has two phases and that the reaction transforming one to the other is
reversible--apparently the crystallization of ice requires removing
some heat.
Frying an egg is an example of an irreversible reaction.
If you dissolve halite in water you can tell that the NaCl is still
present in some form by tasting the water. Why does the NaCl dissolve?
Does it give off heat? Does it require energy?
How is it that diamond, a high-pressure form of C, can coexist
with the low pressure form, graphite, at Earth's surface? Do diamond
and graphite both have the same energy? If you burn graphite and
diamond, which gives you more energy?
When dynamite explodes, why does it change into a rapidly expanding gas, which provides the energy release, plus a few solids?
Chemical thermodynamics provides us with a means of answering these questions and more.
A Few Definitions
A system is any part of the universe we choose to consider.
Matter and energy can flow in or out of an open system but only energy can be added to or subtracted from a closed system. An isolated system is one in which matter and energy are conserved.
A phase is a homogeneous body of matter. The components of a system are defined by a set of chemical formula used to describe the system.
The phase rule:
Extensive parameters are proportional to mass (e.g., V, mass, energy).
Intensive parameters are independent of mass (e.g., P, T); these are the "degrees of freedom" F contained in the phase rule.
Thermodynamics: Power and Limitations
Thermodynamics allows you to predict how chemical systems should behave from a supra-atomic "black-box" level--it says nothing about how chemical systems will behave. Thermodynamics also pertains to the state of a system, and says nothing about the path taken by the system in changing from one state to another.
Chemical Reactions and Equations
How to write chemical reactions; stoichiometry.
Mass and charge balance: e.g., - 2Fe3+ + 3H2O = Fe2O3 + 6H+
Reaction-Produced Change in Mass, Density, Volume
The change in volume  rV of a reaction is the volume V of the products minus the volume of the reactants:
rV of a reaction is the volume V of the products minus the volume of the reactants:
 rV = Vproducts - Vreactants
rV = Vproducts - Vreactants
Thus, if the products are smaller than the reactants,  rV < 0.
rV < 0.
In a generalized reaction such as
 rV = cVC + dVD - aVA - bVB
rV = cVC + dVD - aVA - bVB
This sort of additive relationship is true for other state variables and is usually stated as
where  i are the stoichiometric coefficients, positive for products and negative for reactants.
i are the stoichiometric coefficients, positive for products and negative for reactants.
What Actually Drives Reactions? Is it Energy? Can We Just Calculate
or Measure the Energy Difference of Reactants and Products and Know
Which Way the Reaction Will Go?
For many years people felt that chemical reactions occurred
because the reactants had some kind of energy to give up (i.e., use to
do work)--and that therefore the energy of the products would be less
than the energy of the reactants. However, we all know that when ice
melts it consumes rather than releases heat, so there must be more to
the story behind why chemical reactions occur.
Le Chatelier's Principle
"If a change is made to a system, the system will respond so as to absorb the force causing the change."
Equilibrium
A mechanical analogy for chemical change is that of a ball rolling
down a slope with multiple valleys; we explain the ball's behavior by
saying that mechanical systems have a tendency to reduce their
potential energy.
At equilibrium none of the properties of a system change with time. A system at equilibrium returns to equilibrium if disturbed.
"Stable" describes a system or phase in its lowest energy state.
"Metastable" describes a system or phase in any other energy state.


The figure above shows the mechanical analogy for H2O at -5°C and + 5°C and 1 atm. Left: at -5°C, solid H2O has the lowest possible energy state. Right: at +5°C, liquid H2O has the lowest possible energy state. When solid H2O is actually present at +5°C, the difference between the free energy of solid H2O and liquid H2O is available to drive the reaction to form the stable solid H2O phase, and the reaction will go to completion if kinetically possible.
Energy: How Do We Calculate and Measure Energy and How Can We Use this Knowledge to Predict Reaction Behavior?
Thermodynamics works equally well to describe any kind of work or
energy: magnetic, potential, kinetic, etc. For geological systems we
typically talk about pressure-volume work, which, because mechanical
work is F x, you can imagine might be
x, you can imagine might be
- P
 V
V
or
- V
 P
P
Because we noted that  rV < 0 if the products are smaller than the reactants, we choose to write the P-V work term as
rV < 0 if the products are smaller than the reactants, we choose to write the P-V work term as
- -P
 V
V
so that a decrease in volume - V is seen as positive work or that an increase in volume +
V is seen as positive work or that an increase in volume + V results in a decrease in crystal energy.
V results in a decrease in crystal energy.
The absolute energy of a body can be calculated from Einstein's equation U=mc2, but the presence of the c2
term means that the energy of any system is quite large and that
measuring this energy is impractical. It is more practical to measure
differences in energy  U, and we always discuss or
measure differences relative to some arbitrary standard state.
Analogous to this might be if someone in Namibia asked you to measure
the elevation of the crests of waves at Campus Point--without agreement
on some kind of standard, you wouldn't be able to do much more than
measure the heights of individual waves. If however, you could both
agree on an equivalent "sea level" at both localities, you could then
compare the absolute elevations of the wave crests.
U, and we always discuss or
measure differences relative to some arbitrary standard state.
Analogous to this might be if someone in Namibia asked you to measure
the elevation of the crests of waves at Campus Point--without agreement
on some kind of standard, you wouldn't be able to do much more than
measure the heights of individual waves. If however, you could both
agree on an equivalent "sea level" at both localities, you could then
compare the absolute elevations of the wave crests.
A typical thermodynamic standard state is normal laboratory conditions: 25°C (298.15 K) and 1 atm (often called STP for standard temperature and pressure).
The internal energy U of a mineral is the sum of the potential
energy stored in the interatomic bonds and the kinetic energy of the
atomic vibrations. Thus, you might expect that weakly bonded minerals
have relatively low potential energy and thus low internal energy, and
when a mineral is cold such that its atomic vibrations are slow it will
have low kinetic energy and thus low internal energy. Internal energies
are always defined relative to some non-zero standard state, so we
typically talk about changes in internal energy dU.
| An Aside on Differences and Differentials |
What's the difference among   , d , d , and , and   ? ?
 is used to indicate any kind of difference. is used to indicate any kind of difference.
d is used to indicate a differential.
 is used to indicate a partial differential. For example, the partial differential, with respect to y, of is used to indicate a partial differential. For example, the partial differential, with respect to y, of
f(x,y) = x3y4
is
= 4x3y3
|
First Law of Thermodynamics
Adding heat Q to a crystal increases its internal energy U:
- dU
 dQ
dQ
( indicates 'proportional') but if the
crystal is allowed to expand, some of the added energy will be consumed
by expansion dV, so the total energy of the crystal is reduced:
This is effectively the First Law of Thermo: that total energy (heat + P-V work) is conserved.
indicates 'proportional') but if the
crystal is allowed to expand, some of the added energy will be consumed
by expansion dV, so the total energy of the crystal is reduced:
This is effectively the First Law of Thermo: that total energy (heat + P-V work) is conserved.
Heat Capacity
Heat capacity C describes the amount of heat required to change the temperature of a substance:
- C =

By definition, the heat capacity of water at 15°C is 1 cal K-1 g-1 or 18 cal K-1 mol-1 (i.e., the heat required to heat 1 gram of water from 14.5 to 15.5°C is 1 calorie).
Heat capacities of solids approach zero as absolute zero is approached:
 C = 0
C = 0
The heat capacity is written with a subscript P or V depending on whether it obtains for constant pressure CP or constant volume CV.
As an aside,
- CP = CV + TV
 2/
2/
where  and
and  are the expansivity and compressibility--for solids the difference between CP and CV is minimal and can be ignored as a first approximation. For gases, CP = CV + R, and is quite significant.
are the expansivity and compressibility--for solids the difference between CP and CV is minimal and can be ignored as a first approximation. For gases, CP = CV + R, and is quite significant.
Heat capacities are measured by calorimetry and often fit by a function of the form:
- CP = a + bT + cT-2 + dT-0.5
but there are other expansions for the heat capacity involving more or fewer terms.
Below are some examples of heat capacities of minerals. Note how silicates have a nearly constant heat capacity of ~1 J K-1 g-1 above 400K.

Enthalpy
We have already talked about the familiar concept of heat as energy.
Let's define another measure of energy called enthalpy H--a kind of measure of the thermal energy of a crystal. As we will see below,
Recall that we interpreted
to mean that the internal energy change is the heat change minus the energy lost to relaxation of the crystal. Thus,
means that the enthalpy change is the heat change plus the energy the crystal gains by virtue of not being allowed to expand.
Enthalpy includes the vibrational and bonding energy at absolute zero H0°, plus the energy required to increase temperature:
- H = H0° +
 CPdT
CPdT
i.e., we can find the enthalpy change  H produced by changing temperature by integrating the heat capacity CP:
H produced by changing temperature by integrating the heat capacity CP:
 H =
H =  CPdT
CPdT
| Integration Reminder |
How to integrate the heat capacity (to determine change in enthalpy  H): H):
 CP dT = CP dT =  (a + bT + cT-2 + dT-0.5) (a + bT + cT-2 + dT-0.5)
- =aT + bT2/2 - c/T + 2dT0.5
and is evaluated as
- =a(T2 - T1) + b(T22 - T12)/2 - c(T2-1 - T1-1) + 2d(T20.5 - T10.5)
How to integrate the heat capacity divided by T (to determine entropy S):
  dT = dT =  (a/T + b + cT-3 + dT-1.5) (a/T + b + cT-3 + dT-1.5)
- = a ln T + b T - c T-2/2 - 2 d T -0.5
and is evaluated as
- a(ln T2 - ln T1) + b(T2 - T1) - c(T2-2 - T1-2)/2 - 2d(T2-0.5 - T1-0.5)
Nowadays this will all be done for you by the software you are using.
|
As an example, let's calculate the change in enthalpy  H°298-1000 that results from heating quartz from 298 K to 1000 K, given the following heat capacity expansion coefficients:
H°298-1000 that results from heating quartz from 298 K to 1000 K, given the following heat capacity expansion coefficients:
a = 104.35, b = 6.07E-3, c = 3.4E+4, d = -1070
 (CP dT =
(CP dT =  (a + bT + cT-2 + dT-0.5)
(a + bT + cT-2 + dT-0.5)
- =aT + bT2/2 - c/T + 2dT0.5
evaluated from 298 to 1000K
- =a*(1000-298) + b*(10002-2982)/2 - c*(1000-1-298-1) + 2d*(10000.5-2980.5)
- = 45.37 kJ/mol
Relation Among Enthalpy, Heat, and Heat Capacity ( HP=
HP= QP)
QP)
An important relationship between enthalpy change  H and heat change
H and heat change  Q is revealed by differentiating H = U + PV to obtain the total differential
substituting dU = dQ - PdV we get
dividing by dT gives
at constant pressure,
Q is revealed by differentiating H = U + PV to obtain the total differential
substituting dU = dQ - PdV we get
dividing by dT gives
at constant pressure,  = 0, leaving
= 0, leaving
 =
= 
which is equal to CP:
 =
=  = CP
= CP
Determining Enthalpies
Thus, if we want to measure how the internal energy U of a crystal changes  U with increasing temperature at constant pressure, we want to know
U with increasing temperature at constant pressure, we want to know  H, and we can get that by integrating the heat capacity CP over the temperature range of interest.
H, and we can get that by integrating the heat capacity CP over the temperature range of interest.
There's another way to measure  H, though:
calorimetry. By dissolving a mineral in acid and measuring the heat
produced by the dissolution, we get a heat of dissolution (usually
positive). The enthalpy of "formation"
H, though:
calorimetry. By dissolving a mineral in acid and measuring the heat
produced by the dissolution, we get a heat of dissolution (usually
positive). The enthalpy of "formation"  fH°
of the mineral is then just the opposite of the heat of dissolution
(usually negative). Exceptions to the "usually positive/negative" rule
include CN, HCN, Cu2+, Hg2+, NO, Ag+, and S2-. Enthalpies of formation appear in tables of thermodynamic data and are usually referenced to 298 K and 1 atm.
fH°
of the mineral is then just the opposite of the heat of dissolution
(usually negative). Exceptions to the "usually positive/negative" rule
include CN, HCN, Cu2+, Hg2+, NO, Ag+, and S2-. Enthalpies of formation appear in tables of thermodynamic data and are usually referenced to 298 K and 1 atm.
Enthalpy of Reaction
To get an enthalpy of reaction  rH° we can measure the enthalpies of formation of the reactants and products
rH° we can measure the enthalpies of formation of the reactants and products  fH° and then take the difference between them as
fH° and then take the difference between them as
 rH° =
rH° =  fH°products-
fH°products-  fH°reactants
fH°reactants
For example, we can compute the enthalpy of the reaction
- anhydrite + water = gypsum:
- CaSO4 + 2H2O = CaSO4
 2H2O
2H2O
from
| Ca + S + 2O2 = CaSO4 |
 fH° = -1434.11 kJ/mol fH° = -1434.11 kJ/mol |
| H2 + 0.5O2 = H2O |
 fH° = -285.830 kJ/mol fH° = -285.830 kJ/mol |
Ca + S + 3O2 + 2H2 = CaSO4 2H2O 2H2O |
 fH° = -2022.63 kJ/mol fH° = -2022.63 kJ/mol |
Thus,
 rH° =
rH° =  fH°gypsum -
fH°gypsum -  fH°anhydrite -
fH°anhydrite -  fH°water = -16.86 kJ/mol.
fH°water = -16.86 kJ/mol.
Exothermic vs. Endothermic
If  rH° < 0 the reaction
produces a reduction in enthalpy and is exothermic (heat is given up by
the rock and gained by the surroundings). If
rH° < 0 the reaction
produces a reduction in enthalpy and is exothermic (heat is given up by
the rock and gained by the surroundings). If  rH°
> 0 the reaction produces an increase in enthalpy and is endothermic
(heat from the surroundings is consumed by the rock). An easy way to
remember this is that spontaneous reactions produce a decrease in
internal energy, and because we know that
rH°
> 0 the reaction produces an increase in enthalpy and is endothermic
(heat from the surroundings is consumed by the rock). An easy way to
remember this is that spontaneous reactions produce a decrease in
internal energy, and because we know that
UP  HP
HP
a decrease in HP is also a decrease in UP.
Calculating  fH° at Temperatures Other Than 298 K
fH° at Temperatures Other Than 298 K
So far we know how to calculate the change in enthalpy caused by
heating and we know that we can get enthalpies of formation from
tables. What if we want to know the enthalpy of formation of a mineral
at a temperature other than 298 K?
We do this by calculating  rCP for the reaction that forms the mineral of interest:
rCP for the reaction that forms the mineral of interest:
 rCP =
rCP =  rCPproducts -
rCPproducts -  rCPreactants
rCPreactants
and then integrating. Thus, for example if we want to know  fH° for quartz at 1000 K, we get coefficients for the heat capacities of Si, O2 and SiO2:
fH° for quartz at 1000 K, we get coefficients for the heat capacities of Si, O2 and SiO2:
| compound | a | b | c | d |
|---|
| Si | 31.778 | 5.3878E-4 | -1.4654E5 | -1.7864E2 |
| O2 | 48.318 | -6.9132E-4 | 4.9923E5 | -4.2066E2 |
| SiO2 | 104.35 | 6.07E-3 | 3.4E-4 | -1070 |
for the reaction
and we calculate
 a = 24.254
a = 24.254
 b = 6.2225E-3
b = 6.2225E-3
 c = -3.5E5
c = -3.5E5
 d = -470.7
d = -470.7
and thus,
 fH°1000 -
fH°1000 -  fH°298 =
fH°298 = 
 CP dT =
CP dT =  a*(1000-298) +
a*(1000-298) +  b/2*(10002-2982) -
b/2*(10002-2982) -  c*(1000-1-298-1) + 2
c*(1000-1-298-1) + 2 d*(10000.5-2980.5) = 5.511 kJ/mol
d*(10000.5-2980.5) = 5.511 kJ/mol
This is the change in the enthalpy of formation that results
from heating. We add this to the enthalpy of formation at 298 K to get
the enthalpy of formation at 1000 K:
 fH°1000 = (
fH°1000 = ( fH°1000 -
fH°1000 -  fH°298) +
fH°298) +  fH°298 = 5.511 - 910.700 = -905.2 kJ/mol
fH°298 = 5.511 - 910.700 = -905.2 kJ/mol
In other words, forming quartz from the elements at 1000 K yields slightly less heat than at 298 K.
Compare this with the change in enthalpy  H°298-1000 that results from heating quartz from 298 K to 1000 K, which we calculated is 45.37 kJ/mol.
H°298-1000 that results from heating quartz from 298 K to 1000 K, which we calculated is 45.37 kJ/mol.
Entropy
We have discussed the intuitive statement that reactions probably
proceed because the reactants can decrease their internal energy by
reacting. We also noted that internal energy scales with enthalpy,
suggesting that reactions might 'go' because of a decrease in enthalpy.
However, we then noted that not all reactions give off heat--some, such
as the melting of ice, proceed in spite of consuming heat. Moreover,
there are other processes that proceed in the apparent absence of any
heat change: e.g., mixing of gases or the spreading of dye in water.
What is it that causes these reactions to proceed spontaneously even if
the heat change is zero or endothermic?
The answer is entropy S, which is a measure of the order or disorder.
Entropy has three sources: configurational, electronic, and vibrational.

Electronic entropy arises when an electron in an unfilled orbital can occupy more than one orbital; e.g., for Ti3+, the single 3d electron can occupy one of three possible t2g orbitals and Selectronic = 9 J mol-1 K-1.
Vibrational (or calorimetric) entropy arises because the
energy of lattice vibrations can only increase or decrease in discrete
steps and the energy quanta (phonons) can be distributed within the
possible energy steps in different ways. Vibrational entropy is very
difficult to calculate from statistical mechanics but can be calculated
easily from heat capacity. Here's why:
The entropy of a system always increases during irreversible
processes; i.e., for a reversible process, dS = 0, whereas for
irreversible processes dS >0. This is the Second Law of Thermo--better known as "You can't feed s**t into the rear of a horse and get hay out the front."
If a mineral becomes more ordered during a reaction, reducing its
entropy, the heat liberated must increase the entropy of the
surroundings by an even greater amount. Thus, we write
- dS >

then
 >
> 
and recalling that
- CP =

then
 >
> 
and
- S =

 dT
dT
In other words, the vibrational entropy can be found by integrating the heat capacity divided by temperature.
In a perfectly ordered, pure crystalline material the entropy is zero. This is a simple statement of the Third Law of Thermo, which follows from the fact that heat capacities approach zero at zero K:
 C = 0
C = 0
However, because the rate of atomic diffusion also goes to zero at 0 K, all compounds have some zero-point entropy S°0.
Entropy is thus the only thermodynamic potential for which we can
calculate an absolute value. What we typically do is determine the heat
capacity from near absolute zero to ambient conditions and then
integrate it to get the (absolute) entropy (in fact this gives us only
the vibrational entropy and ignores configurational and electronic
contributions to entropy).


Configurational entropy refers to the entropy resulting from imperfect mixing of different atoms in the same site in a crystal.
When you roll a die, there are six possible outcomes, with the following probability
P(X=1) + P(X=2) + ... + P(X=6) = 1
The probability that any particular number will come up is
- P(X=1) = P(X=2) = ... = P(X=6) = 1/6
The uncertainty associated with that probability is 0 if one outcome
has a probability of 1, and a maximum when the outcomes are equally
likely.
Imagine a material with M atoms that can occupy N sites. If the
mixing is ideal, the atoms have no interaction with each other, so more
than one can occupy the same site. The total number of configurations,  , in this system is
, in this system is
 = NM
= NM
 Copyright c 2009 by C.H. Mak
Copyright c 2009 by C.H. Mak
But, this is slightly incorrect (in what is known as Gibbs' paradox)
because there is overcounting of identical configurations like these

With the overcounting removed we have
 = N! / (Np1! * Np2! ...Npn!)
= N! / (Np1! * Np2! ...Npn!)
where  is the probability that a given number of atoms n in a given number of sites N will have a particular configuration.
Or
is the probability that a given number of atoms n in a given number of sites N will have a particular configuration.
Or
- ln
 = ln N! -
= ln N! -  ln(Npi)!
ln(Npi)!
N is always large where moles of material are concerned, so we can simplify this (using Stirling's approximation: ln (N!) = NlnN - N) to
- ln
 = -N
= -N  pilnpi
pilnpi
For N atomic sites that can contain fraction XA A atoms and XB B atoms,
 =
= 
where  is the probability that a given number of atoms M in a given number of sites N will have a particular configuration.
is the probability that a given number of atoms M in a given number of sites N will have a particular configuration.
Boltzmann defined configurational entropy as
- Sconfigurational = k ln
 (This is engraved on Boltzmann's tomb in Vienna!)
(This is engraved on Boltzmann's tomb in Vienna!)
Simplified with Stirling's approximation (and recalling that R = Nk) to
- S = - n R (XA ln XA + XB ln XB)
where n is the number of sites per mole. For example in
cordierite there are 4 Al atoms and 5 Si atoms distributed over 9
tetrahedral sites. For a random distribution the entropy is
- S = - 9 R (4/9 ln 4/9 + 5/9 ln 5/9) = 51.39 J mol-1 K-1
Note that the form of the configurational entropy equation (and electronic entropy as well) indicates that if XA or XB are 0 or 1, Sconfig is zero:

Entropy Change of Reaction
Just like  rH and
rH and  rV, we can calculate entropies of reactions by using absolute entropies S and calculating a difference in entropy
rV, we can calculate entropies of reactions by using absolute entropies S and calculating a difference in entropy  rS. For example, if we know that
rS. For example, if we know that
- S°CaSO4 = 106.7 J mol-1 K-1
- S°Ca = 41.42 J mol-1 K-1
- S°S = 31.80 J mol-1 K-1
- S°O2 = 205.138 J mol-1 K-1
then the entropy of the reaction
is  rS° = 106.7 - 41.42 - 31.80 - 2 * 205.138 = -376.8 J mol-1 K-1
rS° = 106.7 - 41.42 - 31.80 - 2 * 205.138 = -376.8 J mol-1 K-1
Energy Associated With Entropy
The units of entropy suggest that the energy associated with S scales with temperature:
- dU
 -TS
-TS
(The minus sign is there for reasons similar to the -PV we encountered earlier.)
The energy associated with configurational entropy in the Al4Si5 cordierite we talked about earlier looks like this:

The energy associated with vibrational entropy in tremolite, quartz, and chalcopyrite looks like this:

(Josiah Willard) Gibbs Free Energy of a Phase
The Gibbs free energy G is the thermodynamic potential that
tells us which way a reaction goes at a given set of physical
conditions--neither the enthalpy change nor the entropy change for a
reaction alone can provide us with this information. The two measures
of energy (enthalpy H and entropic energy TS) are brought together in
the Gibbs free energy equation: (the chemical potential is the
equivalent for a component)
which says that the Gibbs free energy G is the internal
energy of the crystal U plus the energy the crystal gains by virtue of
not being allowed to expand minus the entropic energy TS. Recalling
that we can write this in a more understandable way
which says that G is the difference between the heat energy and the entropic energy.

Relationship Among G, S, and V
If we differentiate
to obtain
- dG = dU + PdV + VdP - TdS - SdT
and substitute
(this comes from dS = dQ/T and dU = dQ - PdV); we are left with
meaning that changes in Gibbs free energy are produced by
changes in pressure and temperature acting on the volume and entropy of
a phase.
Realize that when we write
we are implicitly writing
- dG =
 dP -
dP -  dT
dT
which means that
 = V
= V
and
 = -S
= -S
These relations indicate that the change in Gibbs free energy
with respect to pressure is the molar volume V and the change in Gibbs
free energy with respect to temperature is minus the entropy S.
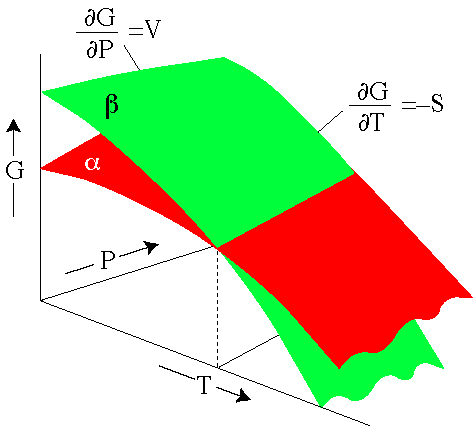
Gibbs Free Energy of Formation
The defining equation for Gibbs free energy
can be written as
such that the Gibbs free energy of formation  fG° is
For example, to calculate the Gibbs free energy of formation of anhydrite, we can use
fG° is
For example, to calculate the Gibbs free energy of formation of anhydrite, we can use
 fH°CaSO4 = -1434.11 kJ/mole
fH°CaSO4 = -1434.11 kJ/mole
- S°CaSO4 = 106.7 J mol-1 K-1
- S°Ca = 41.42 J mol-1 K-1
- S°S = 31.80 J mol-1 K-1
- S°O2 = 205.138 J mol-1 K-1
and we calculate the entropy of formation of anhydrite
 fS° = S°CaSO4 - S°Ca - S°S - 2 * S°O2 = -376.796 J mol-1 K-1
fS° = S°CaSO4 - S°Ca - S°S - 2 * S°O2 = -376.796 J mol-1 K-1
and then use
 fG° =
fG° =  fH° - T
fH° - T fS° = -1434,110 - 298.15 * -376.796 = -1321.77 kJ/mol
fS° = -1434,110 - 298.15 * -376.796 = -1321.77 kJ/mol
Gibbs Free Energy of Reaction
We can write the Gibbs free energy of reaction as the enthalpy change of reaction minus the entropic energy change of reaction
If the heat energy equals the entropic energy
 rH = T
rH = T rS
rS
then
 rG = 0
rG = 0
and there is no reaction. Finally we have come to a
satisfying point--we can now determine whether a given reaction will
occur if we know  H and
H and  S, and both of these are measurable or can be calculated.
S, and both of these are measurable or can be calculated.

If  rG < 0, the Gibbs free energy
of the products is lower than the Gibbs free energy of the reactants
and the reaction moves to produce more products. If
rG < 0, the Gibbs free energy
of the products is lower than the Gibbs free energy of the reactants
and the reaction moves to produce more products. If  rG
> 0, the Gibbs free energy of the products is greater than the Gibbs
free energy of the reactants and the reaction moves to produce more
reactants.
rG
> 0, the Gibbs free energy of the products is greater than the Gibbs
free energy of the reactants and the reaction moves to produce more
reactants.
For example, to calculate  rG° at STP for the reaction
we use
rG° at STP for the reaction
we use
 rH° = 370 J
rH° = 370 J
 rS° = 3.7 J mol-1 K-1
rS° = 3.7 J mol-1 K-1
to calculate
 rG° = 370 - 298.15 * 3.7 = -733 J/mol
rG° = 370 - 298.15 * 3.7 = -733 J/mol
The negative value of  G tells us that calcite has lower Gibbs free energy and that the reaction runs forward (aragonite
G tells us that calcite has lower Gibbs free energy and that the reaction runs forward (aragonite  calcite).
calcite).
Clapeyron Relation
There is a useful relation between the slope of a reaction in PT
space (i.e., dP/dT) and the entropy and volume changes of the reaction
that follows from At equilibrium  G = 0, such that
G = 0, such that
 rVdP =
rVdP =  rSdT
rSdT
or
 =
= 
So, the P-T slope of a reaction is equal to the ratio of the
entropy change to the volume change. Alternatively, along the
equilibrium curve, the changes in pressure times the volume change are
equal to changes in temperature times the entropy change. This is the Clapeyron Equation.

So, a phase diagram is a kind of free energy map.  =
=  along an equilibrium,
along an equilibrium,  <
<  at high P and low T, and
at high P and low T, and  >
>  at high T and low P. Along the equilibrium boundary the Gibbs Free
energies of the reactants and products are equal and the Gibbs Free
energy of reaction
at high T and low P. Along the equilibrium boundary the Gibbs Free
energies of the reactants and products are equal and the Gibbs Free
energy of reaction  rG, is zero.
rG, is zero.
Shortcutting  H and
H and  S and Finding
S and Finding  G Directly
G Directly
Like other thermodynamic potentials, we can write the change in Gibbs free energy of reaction as
 rG° =
rG° =  fG°products-
fG°products-  fG°reactants
fG°reactants
Instead of using  fH° and
fH° and  fS°, it is often possible to obtain
fS°, it is often possible to obtain  fG°
values for most compounds from electronic data bases. For example, if
the following Gibbs free energies of formation are known:
fG°
values for most compounds from electronic data bases. For example, if
the following Gibbs free energies of formation are known:
 fG°CaSO4
fG°CaSO4 2H2O = -1707.280 kJ/mol
2H2O = -1707.280 kJ/mol
 fG°CaSO4 = -1321.790 kJ/mol
fG°CaSO4 = -1321.790 kJ/mol
 fG°H2O = -237.129 kJ/mol
fG°H2O = -237.129 kJ/mol
then for
- CaSO4 + 2H2O = CaSO4
 2H2O
2H2O
 rG° = -1.232 kJ/mol
rG° = -1.232 kJ/mol
Gibbs Free Energy at Any Pressure and Temperature
We know many ways to determine  rG at STP--but how do we calculate
rG at STP--but how do we calculate  rG
for other pressures and temperatures? Recall that the changes in Gibbs
free energy with pressure and temperature are given by two of Maxwell's
relations
If we recast these as
and
rG
for other pressures and temperatures? Recall that the changes in Gibbs
free energy with pressure and temperature are given by two of Maxwell's
relations
If we recast these as
and
and integrate, we get

 rGdP =
rGdP =
 rGP -
rGP -  rGPref =
rGPref =

 rVdP
rVdP
or
and

 rGdT =
rGdT =
 rGT -
rGT -  rGTref = -
rGTref = -

 rSdT
rSdT
or
- ΔrGT = ΔrGTref -
 ΔrSdT
ΔrSdT
thus
 rGPT =
rGPT =  rGPrefTref +
rGPrefTref + 
 rVdP -
rVdP - 
 rSdT
rSdT
Solving the Pressure Integral at Constant Temperature
To a first approximation, we can ignore the expansivity and compressibility of solids and use
as a simplification. Don't forget that this approximation is valid for solids only! An even more common assumption for P>>1 is
For example, calculate the change in Gibbs free energy for the reaction
2 jadeite = albite + nepheline
if pressure increases from 1 bar to 10 kbar, given
 nepheline = 54.16 cm3
nepheline = 54.16 cm3
 albite = 100.43 cm3
albite = 100.43 cm3
 jadeite = 60.40 cm3
jadeite = 60.40 cm3
First we calculate  rV and find
rV and find
 r
r =
=  nepheline +
nepheline +  albite - 2
albite - 2 jadeite = 33.79 cm3 = 3.379 J/bar
jadeite = 33.79 cm3 = 3.379 J/bar
and thus
 rGPT -
rGPT -  rG1,T =
rG1,T =  rVsP = 33.79 kJ/mol
rVsP = 33.79 kJ/mol
Solving the Temperature Integral at Constant Pressure
Recall that the effect of temperature on the entropy change of reaction  rS depends on the heat capacity change of reaction
rS depends on the heat capacity change of reaction  rCP:
Thus
expands to
rCP:
Thus
expands to
 rGT =
rGT =  rGTref
-
rGTref
- 

 STref
+
STref
+ 
 dT
dT dT
dT
If the form of the heat capacity expansion is
- CP = a + bT + cT-2 + dT-0.5
then the above double integral is
 a(T - T ln T)
-
a(T - T ln T)
-  bT2/2
-
bT2/2
-  cT-1/2 + 4
cT-1/2 + 4 dT0.5
-
dT0.5
-
 aTref
-
aTref
-  bTref2/2
+
bTref2/2
+  cTref-1
- 2
cTref-1
- 2 dTref0.5
+
dTref0.5
+
 aTlnTref
+
aTlnTref
+  bTTref
-
bTTref
-  cTTref-2/2
- 2
cTTref-2/2
- 2 dTTref-0.5
- T
dTTref-0.5
- T rSTref
+ Tref
rSTref
+ Tref rSTref
rSTref
Note that this considers only vibrational entropy and ignores configurational entropy. This means of solving for  rG requires that you know
rG requires that you know  rG at the reference temperature.
rG at the reference temperature.
An alternative path that requires that you know the enthalpy change  rH at the reference temperature is
rH at the reference temperature is
 rGT =
rGT =
 rHTref
+
rHTref
+ 
 CPdT - T
CPdT - T
 rSTref
+
rSTref
+ 
 dT
dT
Solving the Temperature and Pressure Integrals for  rGP,T
rGP,T
To calculate the Gibbs free energy change of a reaction at any
pressure and temperature, we can use either of the following equations,
depending on whether we know  rH or
rH or  rG
rG
 rGP,T =
rGP,T =  rG1,Tref
-
rG1,Tref
- 

 rSTref
+
rSTref
+ 
 dT
dT dT
+
dT
+  rVsP
rVsP
 rGP,T =
rGP,T =
 rH1,Tref
+
rH1,Tref
+ 
 CPdT - T
CPdT - T
 rSTref
+
rSTref
+ 
 dT
dT +
+  rVsP
rVsP
If you don't have heat capacity data for the reaction of interest, these equations can be roughly approximated as
 rGP,T =
rGP,T =  rG1,Tref
-
rG1,Tref
-  rS1,Tref(T - Tref)
+
rS1,Tref(T - Tref)
+  rVsP
rVsP
 rGP,T =
rGP,T =
 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
+
rS1,Tref
+  rVsP
rVsP
For example, calculate  rG for jadeite + quartz = albite at 800 K and 20 kbar. The data at 298 K and 1 bar are
rG for jadeite + quartz = albite at 800 K and 20 kbar. The data at 298 K and 1 bar are
 rH° = 15.86 kJ/mol
rH° = 15.86 kJ/mol
 rS° = 51.47 J K-1 mol-1
rS° = 51.47 J K-1 mol-1
 rVs° = 1.7342 J/bar = 17.342 cm3/mol
rVs° = 1.7342 J/bar = 17.342 cm3/mol
Using
 rGP,T =
rGP,T =
 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
+
rS1,Tref
+  rVsP
rVsP
- = 15,860 - 800 * 51.47 + 1.7342 * 20,000 = 9.37 kJ/mol
If we had used the complete equation for solids, integrating
the heat capacities, we would have obtained an answer of 9.86
kJ/mol--not horrifically different.
Calculating the PT Position of a Reaction
If we say that  rG = 0 at equilibrium, then we can write our solids-only and constant-heat-capacity approximations as
rG = 0 at equilibrium, then we can write our solids-only and constant-heat-capacity approximations as
- 0 =
 rG1,T
-
rG1,T
-  rS1,Tref(T - Tref)
+
rS1,Tref(T - Tref)
+  rVsP
rVsP
- 0 =
 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
+
rS1,Tref
+  rVsP
rVsP
and thus we can calculate the pressure of a reaction at different temperatures by
- P =

 rG1,Tref
-
rG1,Tref
-  rS1,Tref(T - Tref)
rS1,Tref(T - Tref) / -
/ - rVs
rVs
- P =

 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
rS1,Tref / -
/ - rVs
rVs
and we can calculate the temperature of a reaction at different pressures by
- T = Tref +

 rG1,Tref +
rG1,Tref +  rVsP
rVsP /
/  rS1,Tref
rS1,Tref
- T = Tref +

 rH1,Tref
+
rH1,Tref
+  rVsP
rVsP /
/  rS1,Tref
rS1,Tref
Let's do this for the albite = jadeite + quartz reaction at T = 400 K and T = 1000 K:
- P = (15,860 - 5147 * 400) / -1.7342 = 2.7 kbar
- P = (15,860 - 5147 * 1000) / -1.7342 = 20.6 kbar
Assuming that dP/dT is constant (a bad assumption, we know), the reaction looks like this

Solutions
Almost no phases are pure, but typically are mixtures of components. For example, olivine varies from pure forsterite Mg2SiO4 to pure fayalite Fe2SiO4, and can have any composition in between--it is a solid solution. We need a way to calculate the thermodynamic properties of such solutions.
As a measure of convenience, we use mole fraction to describe the
compositions of phases that are solid solutions. For example, a mix of
1 part forsterite and 3 parts fayalite yields an olivine with 25 mol%
forsterite and 75 mol% fayalite, which can be written as (Mg0.25Fe0.75)2SiO4 or fo25fa75, etc. Mole fractions are denoted as Xi.
We need a way of splitting up the Gibbs free energy of a phase
among the various components of the phase--how for example do we decide
how much of the Gibbs free energy of an olivine is related to the
forsterite component and how much derives from the fayalite component?
Likewise, how does the Gibbs free energy of a phase vary with
composition--is the relationship linear between endmembers?? We address
these issues by defining a partial Gibbs free energy for each component
at constant pressure and temperature and constant composition of other
components, called the partial molar Gibbs free energy or chemical potential
- μi =

where n is the amount of substance. For olivine solid
solution composed of fayalite and forsterite components or endmembers,
we write
- dG =
 dnfayalite +
dnfayalite +  dnforsterite
dnforsterite
Volume of Mixing
Imagine that mole fractions of phase A and phase B with molar volumes VA and VB, are mixed together. We can describe the volume of the mixture as
and it is a linear mixing of the two endmember volumes. We call this ideal mixing or mechanical mixing. Real solutions, however, do not behave this way, and the mixing is always non ideal,
although sometimes only weakly so. The figure shows mixing that
produces a smaller volume than expected, but it is not possible to
predict the shapes and positions of such mixing curves.

in this figure, the molar volumes of the endmembers are VAo and VBo, and the partial molar volumes are  A and
A and  B.
B.
Partial Molar Volume
The partial molar volume is defined as
 i
i
If you mix two compounds A and B together and find a volume
of mixing that is non-ideal, how can you determine the contribution
that A and B each make to the volume? That is, what are the partial molar volumes of A and B,  A and
A and  B?
Graphically, the partial molar volumes are the A and B axis intercepts
of the tangent to the mixing curve, and can be described by the simple
relationship:
B?
Graphically, the partial molar volumes are the A and B axis intercepts
of the tangent to the mixing curve, and can be described by the simple
relationship:
- Vmix = XA
 A + XB
A + XB B
B
or
- Vmix =
 Xi
Xi i
i
The behavior of this function is such that when XA is 1, Vmix = VA and when XA is 0, Vmix = VB = VBo. Alternatively,
-
 A = (Vmix - XB
A = (Vmix - XB B) / XA
B) / XA
Entropy of Mixing
The entropy of mixing is never zero because mixing increases
entropy. As we discussed days ago, the entropy of mixing (i.e., the
configurational entropy) is
 Smix = -R
Smix = -R  (Xi ln Xi)
(Xi ln Xi)
where i = 1..n is the number of sites over which mixing is occurring.
Enthalpy of Mixing
Enthalpies also do not combined ideally (linearly) in mixtures
because the mixture may have stronger bonds than were present in either
of the unmixed phases. The excess enthalpy is  Hmix = 0.5 * N z XAXB [2
Hmix = 0.5 * N z XAXB [2 AB -
AB -  AA -
AA -  BB]
BB]
where  AB is the interaction energy among A-B atoms,
AB is the interaction energy among A-B atoms,  AA is the interaction energy among A-A atoms, and
AA is the interaction energy among A-A atoms, and  BB is the interaction energy among B-B atoms.
BB is the interaction energy among B-B atoms.
Gibbs Free Energy of Mixing
Recall that all spontaneous processes/reactions occur because of a
decrease in Gibbs free energy. It should therefore not surprise you
that the Gibbs free energy of mixing is always negative--otherwise
mixing would not occur. The fact that μA < G°A and μB < G°B illustrates why compounds combine spontaneously--each compound is able to lower its free energy.

The above figure is hypothetical because we cannot measure or
calculate the absolute Gibbs free energy of phases. For this reason, μ is always expressed as a difference from some standard state measurement, as  μ, μ - μ°, or μ - G°.
μ, μ - μ°, or μ - G°.
The difference between the absolute Gibbs free energy G° per mole μ° of a pure compound and the chemical potential per mole μ of dissolved compound (i.e., the difference between the blue and red curves in the above figure) is
 A - G°A =
A - G°A =  A -
A -  °A = RT lnXA
°A = RT lnXA B - G°B =
B - G°B =  B -
B -  °B = RT lnXB
°B = RT lnXB
This function has the following shape:

implying that when the mineral is pure (X = 1) then  μ
= 0, and when the mineral is infinitely dilute (X = 0), the chemical
potential is undefined. For example, in a two-component mineral if XA = 0.4, at T = 298 K,
μ
= 0, and when the mineral is infinitely dilute (X = 0), the chemical
potential is undefined. For example, in a two-component mineral if XA = 0.4, at T = 298 K,
- μA - μ°A = 8.314 * 298 ln 0.4 = -2271 J
- μB - μ°B = 8.314 * 298 ln 0.6 = -1266 J
The equation of the  Gmix line is the sum of the chemical potentials of the endmembers:
Gmix line is the sum of the chemical potentials of the endmembers:
 Gmix = RT (XA ln XA + XB ln XB) or
Gmix = RT (XA ln XA + XB ln XB) or
 Gmix = RT
Gmix = RT  (Xi ln Xi)
(Xi ln Xi)
which looks like this for two components:

Actually, all this discussion has been predicated on the assumption that  Hmix = 0. If this is not true,
Hmix = 0. If this is not true,  Gmix is not a simple function of composition, but has the general form:
Gmix is not a simple function of composition, but has the general form:

Depending on the relative values of  Hmix and -T
Hmix and -T Smix,
the free energy of mixing may be negative throughout the whole
composition range if the entropic energy contribution outweighs the
enthalpy increase; this is more likely at higher temperature.
Smix,
the free energy of mixing may be negative throughout the whole
composition range if the entropic energy contribution outweighs the
enthalpy increase; this is more likely at higher temperature.
The two free energy minima in the above figure indicate that
minerals of intermediate compositions can reduce their free energy by
unmixing into two phases. This explains the appearance and driving
force for exsolution. Note that this can only be true if  Hmix > 0, i.e., if 2
Hmix > 0, i.e., if 2 AB >
AB >  AA +
AA +  BB,
which makes sense because it means that the A-B bonds have a higher
free energy than the sum of the free energies of separate AA and BB
bonds.
BB,
which makes sense because it means that the A-B bonds have a higher
free energy than the sum of the free energies of separate AA and BB
bonds.
Activities
In reality, no phases behave ideally--that is, their chemical
potentials are never simple logarithmic functions of composition as
implies. Instead, we say that the chemical potential is a simple logarithmic function of activity and define activity as
a = ( X)
X)
where a is the activity of a compound,  is the "site occupancy coefficient" (e.g.,
is the "site occupancy coefficient" (e.g.,  = 2 for Mg in Mg2SiO4), and
= 2 for Mg in Mg2SiO4), and  is the activity coefficient that describes the non-ideal behavior. Thus we write
For pure compounds a=1 because X=1. For ideal compounds
is the activity coefficient that describes the non-ideal behavior. Thus we write
For pure compounds a=1 because X=1. For ideal compounds  =1.
As a specific example, the chemical potential of the almandine (Fe3Al2Si3O12) component of a garnet solid solution ((Fe, Mg, Ca, Mn)3Al2Si3O12) is
To be clear, μ° is the chemical potential of the component in its pure reference state and varies as a function of pressure and temperature; this we measure with calorimetry. μ is the chemical potential as it actually occurs and varies as a function of phase composition; this we measure with an electron microprobe. The activity forms a bridge between idealized behavior and real behavior.
=1.
As a specific example, the chemical potential of the almandine (Fe3Al2Si3O12) component of a garnet solid solution ((Fe, Mg, Ca, Mn)3Al2Si3O12) is
To be clear, μ° is the chemical potential of the component in its pure reference state and varies as a function of pressure and temperature; this we measure with calorimetry. μ is the chemical potential as it actually occurs and varies as a function of phase composition; this we measure with an electron microprobe. The activity forms a bridge between idealized behavior and real behavior.
The Equilibrium Constant
At equilibrium the sum of the Gibbs free energies of the reactants
equals the sum of the Gibbs free energies of the products. Equally, the
sum of the partial molar Gibbs free energies (chemical potentials) of
the reactants equals the sum of the partial molar Gibbs free energies
(chemical potentials) of the products. In other words, for at equilibrium,
More generally, for
then
or, at equilibrium
 rμ = 0 = cμC + dμD - aμA - bμB
rμ = 0 = cμC + dμD - aμA - bμB
which we can reformat as
where  i is the
stochiometric coefficient of a product or reactant and is positive if
for a product and negative if for a reactant. If we then remember that and rewrite it as
we can reformat the earlier equation as
i is the
stochiometric coefficient of a product or reactant and is positive if
for a product and negative if for a reactant. If we then remember that and rewrite it as
we can reformat the earlier equation as
 rμ = 0 = c(μC° + RT lnaC) + d(μD° + RT lnaD) - a(μA° + RT lnaA) - b(μB° + RT lnaB)
rμ = 0 = c(μC° + RT lnaC) + d(μD° + RT lnaD) - a(μA° + RT lnaA) - b(μB° + RT lnaB)
which looks nicer as
 rμ =
rμ =  rμ° + RT ln (aCc aDd/aAa aBb)
rμ° + RT ln (aCc aDd/aAa aBb)
To be completely general we write
 rμ =
rμ =  rμ° + RT ln
rμ° + RT ln  ai
ai (
( means to multiply all i terms)
means to multiply all i terms)
This equation is invariably simplified to
 rμ =
rμ =  rμ° + RT lnQ
rμ° + RT lnQ
and Q is the activity product ratio. The activities in the Q term change as the reaction progresses toward equilibrium.
To be clear again,  rμ°
is the difference in the Gibbs free energies of the products and
reactants when each is in its pure reference state and varies as a
function of pressure and temperature.
rμ°
is the difference in the Gibbs free energies of the products and
reactants when each is in its pure reference state and varies as a
function of pressure and temperature.  rμ is the difference in the Gibbs free energies of the products and reactants as they actually occur and varies as a function of phase composition.
rμ is the difference in the Gibbs free energies of the products and reactants as they actually occur and varies as a function of phase composition.
At equilibrium, the product and reactant activities have adjusted themselves such that  rμ = 0. We write this (with K instead of Q, to signify equilibrium) as
rμ = 0. We write this (with K instead of Q, to signify equilibrium) as
- 0 =
 rG° = -RT ln K
rG° = -RT ln K
K is called the equilibrium constant. If K is very large (ln
K positive), the combined activities of the reaction products are
enormous relative to the combined activities of the reactants and the
reaction will likely progress. On the other hand, if K is small (ln K negative), there is unlikely to be any reaction.
The utility of K is that it tells us for any reaction and any
pressure and temperature, what the activity ratios of the phases will
be at equilibrium. For example, for the reaction
- albite = jadeite + quartz
let's say that at a particular P and T,
 rG° = -20.12 kJ/mol
rG° = -20.12 kJ/mol
Using
 rG° = -RT lnK
rG° = -RT lnK
we calculate
This means that at equilibrium,
- (ajadeite aquartz / aNaAlSi3O8) = e3.52
Where ajadeite is the activity of NaAlSi2O6 in clinopyroxene and aalbite is the activity of NaAlSi3O8 in plagioclase.
Graphical Portrayal of K
Another way to write the activity product ratio is
or
At equilibrium, where ΔrG°= 0, ln K = 0 and K = 1. Let's see what K looks like for jadeite + quartz = albite at 800 K and 20 kbar:
- ln K = - (ΔrH1,Tref
- TΔrSTref
+ ΔrVsP)/ RT
- = -(15,860 - 800 * 51.47 + 1.7342 * 20,000)/(8.314*800) = -1.4
If we do this for all of PT space, we can contour PT space in terms of lnK:


Alternative Route to the Equilibrium Constant
When we think of mass balance in a reaction, we can explicitly write
- 0 =

 iMi
iMi
where  i are the stoichiometric coefficients and Mi are the masses or the phase components. Analogously, we can explicitly write a similar balance among the chemical potentials:
i are the stoichiometric coefficients and Mi are the masses or the phase components. Analogously, we can explicitly write a similar balance among the chemical potentials:
- 0 =

 iμi
iμi
For each chemical potential we can write
Combining these two equations we find
- 0 =

 iμ°i +
iμ°i + 
 iRTln ai
iRTln ai
- 0 =

 iμ°i +
iμ°i +  RTln (ai)
RTln (ai)
- 0 =

 iμ°i + RTln
iμ°i + RTln  ai
ai
- 0 =

 iμ°i + RTln K
iμ°i + RTln K
and eventually
- 0 =
 rG° + RT ln K
rG° + RT ln K
or
 rG° = -RT ln K
rG° = -RT ln K
The equation
- K =
 ai
ai
is the law of mass action (which actually discusses the action of chemical potential rather than mass). We can also write for 298 K and 1 atm
 rH° - T
rH° - T rS° = - RT ln K
rS° = - RT ln K
and for any P and T of interest:
 rH1,Tref
+
rH1,Tref
+ 
 CPdT - T
CPdT - T
 rSTref
+
rSTref
+ 
 dT
dT +
+ 
 rVP = - RT ln K
rVP = - RT ln K
This has been called "the most important equation in
thermodynamics," so you'd better like it(!) The equilibrium constant K
is a function of 1/T
- -ln K = (
 rG° / RT) = [(
rG° / RT) = [( rH / RT) - (
rH / RT) - ( rS / R)]
rS / R)]
Which looks like

Activity Models (Activity-Composition Relations) for Crystalline Solutions
Garnets are solid solutions of
| component | abbrev. | formula |
|---|
| pyrope | prp | Mg3Al2Si3O12 |
| almandine | alm | Fe3Al2Si3O12 |
| grossular | grs | Ca3Al2Si3O12 |
| spessartine | sps | Mn3Al2Si3O12 |
| andradite | and | Ca3Fe23+Si3O12 |
Mixing models derive from entropy considerations. In particular the relation
 Smix = -R
Smix = -R  Xi ln Xi
Xi ln Xi
although we will not go through the derivation.
Mixing on a Single Site
The simplest type of useful activity model is the ionic model,
wherein we assume that mixing occurs on crystallographic sites. For a
Mg-Fe-Ca-Mn garnet with mixing on one site, which we can idealize as
(A,B,C,D) Al2Si3O12, the activities are
Al2Si3O12, the activities are
- aprp =
 Mg3XMg3
Mg3XMg3
- aalm =
 Fe3XFe3
Fe3XFe3
- agrs =
 Ca3XCa3
Ca3XCa3
- asps =
 Mn3XMn3
Mn3XMn3

The form of a cubic ideal activity model is shown in the above figure.
In general, for ideal mixing in a mineral with a single crystallographic site that can contain  ions,
ions,
- ai = Xj

where a, the activity of component i, is the mole fraction of element j raised to the  power. For non-ideal mixing, we include an activity coefficient
power. For non-ideal mixing, we include an activity coefficient 
Mixing on a Several Sites
For minerals with two distinct sites and the general formula
- (A,B)
 (Y,Z)
(Y,Z)
there are four possible end member components A Y
Y , A
, A Z
Z , B
, B Y
Y , and B
, and B Z
Z .
.
The ideal activities of these components are
- aA
 Y
Y = XA
= XA XY
XY
- aA
 Z
Z = XA
= XA XZ
XZ
- aB
 Y
Y = XB
= XB XY
XY
- aB
 Z
Z = XB
= XB XZ
XZ
For non-ideal garnet activities we write
- aprp = XMg3 XAl2
or
 Mg3 XMg3
Mg3 XMg3
 Al2 XAl2
Al2 XAl2
- aalm = XFe3 XAl2
or
 Fe3 XFe3
Fe3 XFe3
 Al2 XAl2
Al2 XAl2
- agrs = XCa3 XAl2
or
 Ca3 XCa3
Ca3 XCa3
 Al2 XAl2
Al2 XAl2
- asps = XMn3 XAl2
or
 Mn3 XMn3
Mn3 XMn3
 Al2 XAl2
Al2 XAl2
- aand = XCa3 XFe3+2
or
 Ca3 XMn3
Ca3 XMn3
 Fe3+2 XFe3+2
Fe3+2 XFe3+2
where the X3 term describes mixing on the 8-fold trivalent site and the X2 term describes mixing on the octahedral divalent site.

The pyrope activity is shown in the above figure for Mg from 0  3 and Al from 0
3 and Al from 0  2.
2.
It is common to modify such models--that are based on completely
random mixing of elements--with models that consider local charge
balance on certain sites or the Al-avoidance principle.
Geothermometry and Geobarometry
Exchange Reactions
Many thermometers are based on exchange reactions, which are reactions that exchange elements but preserve reactant and product phases. For example:
|
+ KMg3AlSi3O10(OH)2 |
= Mg3Al2Si3O12 |
+ KFe3AlSi3O10(OH)2 |
|
+ phlogopite |
= pyrope |
+ annite |
We can reduce this reaction to a simple exchange vector:
- (FeMg)gar+1 = (FeMg)bio-1
Popular thermometers include garnet-biotite (GARB),
garnet-clinopyroxene, garnet-hornblende, and
clinopyroxene-orthopyroxene; all of these are based on the exchange of
Fe and Mg, and are excellent thermometers because  rV is small, such that
rV is small, such that
 =
= 
is large (i.e., the reactions have steep slopes and are
little influenced by pressure). Let's write the equilibrium constant
for the GARB exchange reaction - K = (aprpaann)/(aalmaphl)
thus
 rG = -RT ln (aprpaann)/(aalmaphl)
rG = -RT ln (aprpaann)/(aalmaphl)
This equation implies that the activities of the Fe and
Mg components of biotite and garnet are a function of Gibbs free energy
change and thus are functions of pressure and temperature.
If we assume ideal behavior ( = 1) in garnet and biotite and assume that there is mixing on only 1 site
= 1) in garnet and biotite and assume that there is mixing on only 1 site
- aalm = Xalm3 = [Fe/(Fe + Mg + Ca + Mn)]3
- aprp = Xprp3 = [Mg/(Fe + Mg)]3
- aann = Xann3 = [Fe/(Fe + Mg)]3
- aphl = Xphl3 = [Mg/(Fe + Mg)]3
Thus the equilibrium constant is
- K = (XMggar XFebio)/(XFegar XMgbio)
When discussing element partitioning it is common to define a distribution coefficient KD,
which is just the equilibrium constant without the exponent (this just
describes the partitioning of elements and not the partitioning of
chemical potential):
- KD = (XMggar XFebio)/(XFegar XMgbio) = (Mg/Fe)gar /(Mg/Fe)bio = K1/3
Long before most of you were playground bullies (1978) a
couple of deities named John Ferry and Frank Spear measured
experimentally the distribution of Fe and Mg between biotite and garnet
at 2 kbar and found the following relationship:

If you compare their empirical equation
- ln KD = -2109 / T + 0.782
this immediately reminds you of
- ln K = - (
 rG° / RT) = -(
rG° / RT) = -( rH / RT) - (P
rH / RT) - (P rV / RT) + (
rV / RT) + ( rS / R)
rS / R)
and you realize that for this reaction
 rS = 3*0.782*R = 19.51 J/mol K
rS = 3*0.782*R = 19.51 J/mol K
(the three comes from the site occupancy coefficient; i.e., K = KD3) and
- -(
 rH / R) - (P
rH / R) - (P rV / R) = -2109
rV / R) = -2109
or
 rH = 3*2109*R -2070*
rH = 3*2109*R -2070* rV
rV
Molar volume measurements show that for this exchange reaction  rV = 0.238 J/bar, thus
rV = 0.238 J/bar, thus
 rH = 52.11 kJ/mol
rH = 52.11 kJ/mol
The full equation is then
- 52,110 - 19.51*T(K) + 0.238*P(bar) + 3RT ln KD = 0
To plot the KD lines in PT space

Net-Transfer Reactions
Net-transfer reactions are those that cause phases to appear or
disappear. Geobarometers are often based on net-transfer reactions
because  rV is large and relatively insensitive to temperature. A popular one is GASP:
rV is large and relatively insensitive to temperature. A popular one is GASP:
| 3CaAl2Si2O8 |
= Ca3Al2Si3O12 |
+ 2Al2SiO5 |
+ SiO2
|
| anorthite |
= grossular |
+ kyanite |
+ quartz |
which describes the high-pressure breakdown of anorthite.

For this reaction
 rG
= -RT ln [(aqtzaky2agrs) / aan3]
= -RT ln agrs / aan3
rG
= -RT ln [(aqtzaky2agrs) / aan3]
= -RT ln agrs / aan3
(the activities of quartz and kyanite are one because they
are pure phases). A best fit through the experimental data for this
reaction by Andrea Koziol and Bob Newton yields
- P(bar) = 22.80 T(K) - 7317
for  rV = -6.608 J/bar. Again, if we use
rV = -6.608 J/bar. Again, if we use
- ln K = -(
 rH / RT) - (P
rH / RT) - (P rV / RT) + (
rV / RT) + ( rS / R)
rS / R)
and set ln K = 0 to calculate values at equilibrium, we can rewrite the above as
- (P
 rV / R) = -(
rV / R) = -( rH / R) + (T
rH / R) + (T rS / R)
rS / R)
or
if T rS /
rS /  rV = 22.8 then
rV = 22.8 then  rS = -150.66 J/mol K
rS = -150.66 J/mol K
if  rH /
rH /  rV = 7317 then
rV = 7317 then  rH = -48.357 kJ/mol
rH = -48.357 kJ/mol
So, we can write the whole shmear as
- 0 = -48,357 + 150.66 T(K) -6.608 P (bar) + RT ln K
Contours of ln K on a PT diagram for GASP look like this:

Kinetics
Thermodynamics places no constraints on the rate or mechanism of
reaction--that is the realm of kinetics. A popular method for
describing the rate at which reactions proceed is to talk of an activated state through which the reaction must pass:

When a system passes from an initial to a final state it must overcome an activation energy barrier  G*.
G*.
The advantages of this activation energy barrier paradigm are that it qualitatively explains the i) persistence of metastable states; ii) effect of catalysts in lowering  G*;
iii) temperature dependence of transformation. We can draw a similar
diagram for a change in enthalpy induced by the reaction
G*;
iii) temperature dependence of transformation. We can draw a similar
diagram for a change in enthalpy induced by the reaction  rH and an activation enthalpy barrier
rH and an activation enthalpy barrier  H* (usually called an activation energy Q*). Of course, unlike
H* (usually called an activation energy Q*). Of course, unlike  rG,
rG,  rH can be positive or negative:
rH can be positive or negative:

It is not easy to generalize about the activation entropy  S*, however, in general, reactions with positive entropy change
S*, however, in general, reactions with positive entropy change  rS
are faster. For example, evaporation is faster than condensation,
melting is faster than crystallization, and disordering is faster than
ordering.
rS
are faster. For example, evaporation is faster than condensation,
melting is faster than crystallization, and disordering is faster than
ordering.
Because thermal energy dictates whether an atom has sufficient
energy to overcome an activation energy barrier, we will write that the
fraction of atoms with thermal energy greater than  H* is
H* is
- f = exp ( -
 H*/RT)
H*/RT)
i.e., if f << 1, few atoms have enough thermal energy
to overcome the activation energy barrier, whereas if f = 1 all atoms
can overcome the activation energy barrier. 
For reactions that involve a single step characterized by a
single activation energy, the rate of the reaction depends on the i)
frequency with which atoms attempt to jump from one site to the next  ;
ii) fraction of atoms with thermal energy greater than Q*; and iii)
probability p that the atom jumping satisfies some geometrical
consideration (this is a fancy name for a fudge factor):
;
ii) fraction of atoms with thermal energy greater than Q*; and iii)
probability p that the atom jumping satisfies some geometrical
consideration (this is a fancy name for a fudge factor):
-
rate
 p
p  exp(-Q*/RT)
exp(-Q*/RT)
Often this is rewritten as
rate  (kT/h)
(kT/h)  exp(-Q*/RT)
where k is Boltzmann's constant, and h is Planck's constant. Thus, the rate
exp(-Q*/RT)
where k is Boltzmann's constant, and h is Planck's constant. Thus, the rate  at which atoms jump is related to temperature and to atom-scale processes described by k and h.
at which atoms jump is related to temperature and to atom-scale processes described by k and h.
Nucleation
Most transformations take place by nucleation and growth. The
driving force for nucleation results from the fact that the formation
of the new phase lowers the total free energy by  VG, the Gibbs free energy change of reaction per unit volume. Nucleation is opposed by an interfacial energy
VG, the Gibbs free energy change of reaction per unit volume. Nucleation is opposed by an interfacial energy  and a strain energy
and a strain energy  . The overall change in nucleation energy for a spherical nucleus of radius r is then
. The overall change in nucleation energy for a spherical nucleus of radius r is then
 nG =
nG =  VG +
VG +  Ginterfacial +
Ginterfacial +  Gstrain = (4/3)
Gstrain = (4/3) r3
r3 VG + 4
VG + 4  r2
r2 + (4/3)
+ (4/3) r3
r3
These different energy contributions yield an increase in total free energy up to a certain radius termed the critical radius, beyond which the total free energy decreases.

This change from increasing to decreasing nucleation free energy
happens because the surface:volume ratio decreases with increasing
radius, so the negative volume free energy term that favors nucleation
eventually overwhelms the positive surface and strain free energy terms
that oppose nucleation. We can re-order the terms in the above equation
to calculate the critical size of the nucleus rc
If, at the critical radius,  nG =
nG =  G*, the activation energy for nucleation is
G*, the activation energy for nucleation is
Growth
Following nucleation, grains of the product phase(s) grow to
replace the parent phase(s). Either the reaction is polymorphic, or
atoms of the parent phase must dissolve, be transported, and then
attach themselves to the product phase. The rate of growth is thus
controlled by the rate of the slowest of these three steps, and is
described as either interface controlled or diffusion controlled.
Turnbull's (1956) formulation to quantify interface-controlled growth rate  is:
is:
 =
=  (kT/h) exp( -Q*/RT)[( -
(kT/h) exp( -Q*/RT)[( - rG/RT)]
rG/RT)]
where  is an "interface jump distance" and the rest you will recognize from previous equations. The [( -
is an "interface jump distance" and the rest you will recognize from previous equations. The [( - rG/RT)] term indicates that the rate of growth depends on the Gibbs free energy change of reaction. As
rG/RT)] term indicates that the rate of growth depends on the Gibbs free energy change of reaction. As  rG
rG  0, this term also approaches zero. As
0, this term also approaches zero. As  rG
rG 
 , this term approaches 1.
, this term approaches 1.
Transformation: Nucleation + Growth
A complete transformation involves nucleation and growth--the
product phases must form and grow and the parent phases must be
consumed. The letter _ is often used to indicate 'reaction progress' or
'degree of transformation,' and varies from 0 (no reaction) to 1
(complete reaction). The transformation is the time-integrated result
of ongoing nucleation and growth, which can vary in time and space:
Just as an example, the general rate equation for
interface-controlled (i.e., not diffusion-controlled) growth of nuclei
formed on grain boundaries is
 = 1 - exp{(6.7/d)
= 1 - exp{(6.7/d) [1-exp(
[1-exp(

 [
[ 2(t -
2(t -  )2 - y2] d
)2 - y2] d )] dy}
)] dy}
In their simplest form, these equations have the form
 = 1 - exp(-ktn)
= 1 - exp(-ktn)
Flip this around to
- exp(-ktn) = 1 -

linearize by means of logarithms
- -ktn = ln (1 -
 )
)
change signs and cleverly insert ln 1
- ktn = ln 1 - ln (1 -
 )
)
rewrite the two logarithms as one, recalling that ln (a/b) = ln a - ln b
- ktn = ln [1 / (1 -
 )]
)]
and linearize once more with logarithms to get the final glorious equation
- n ln t + ln k = ln [ ln (1 -
 )]
)]
The Last Supper: A Still Life of Thermodynamics & Kinetics
Zeolites, like laumontite and wairakite, form in oil fields as
alteration products of plagioclase and other Ca-bearing phases. The
thermodynamic properties ( H, S, V, CP) of zeolites have been measured, and we can use those properties to calculate a phase diagram for the CASH system:
H, S, V, CP) of zeolites have been measured, and we can use those properties to calculate a phase diagram for the CASH system:
Laumontite is the phase that is stable at the lowest P and T.
Wairakite is the next phase to form, and it does so via the reaction
laumontite _ wairakite + H2O. At higher temperature wairakite + H2O decompose to anorthite + quartz + H2O.
Kinetic experiments conducted on the reaction laumontite _ wairakite + H2O, using crystals of laumontite suspended in H2O, reveal the transformation vs. time data in the figure above.
One could use the equation
to interpret the two sub-figures to reveal different n and k values
for each temperature. This is the way rate data were interpreted in the
bad old days, but this approach lacks any physical or mechanistic
basis. Instead, we can measure the rate of growth at each temperature
and relate the rate of growth to the Turnbull equation. Above is an
example of grain growth data collected for 450°C. The rate of growth is
interpreted to be a constant 2.0 ± 0.3 E-10 m/s. If growth rate data
like this can be collected for every temperature of interest, an
activation energy for growth can be calculated:
The activation energy for growth apparently varies from ~196 kJ/mol
to ~ 72 kJ/mol depending on the reaction mechanism. The growth rate
data can be combined with similar nucleation rate data to yield a
complete transformation rate equation that can be extrapolated to
geologic conditions of interest. The figure below shows extrapolated
growth rates (m/s) for the laumontite _ wairakite + H2O reaction.
 rV = Vproducts - Vreactants
rV = Vproducts - Vreactants
 rV of a reaction is the volume V of the products minus the volume of the reactants:
rV of a reaction is the volume V of the products minus the volume of the reactants:
 rV = Vproducts - Vreactants
rV = Vproducts - Vreactants
 rV < 0.
rV < 0.
 rV = cVC + dVD - aVA - bVB
rV = cVC + dVD - aVA - bVB
 r
r

 i
i i
i
 i are the stoichiometric coefficients, positive for products and negative for reactants.
i are the stoichiometric coefficients, positive for products and negative for reactants.


 x, you can imagine might be
x, you can imagine might be
 V
V
 P
P
 rV < 0 if the products are smaller than the reactants, we choose to write the P-V work term as
rV < 0 if the products are smaller than the reactants, we choose to write the P-V work term as
 V
V
 V is seen as positive work or that an increase in volume +
V is seen as positive work or that an increase in volume + V results in a decrease in crystal energy.
V results in a decrease in crystal energy.
 U, and we always discuss or
measure differences relative to some arbitrary standard state.
Analogous to this might be if someone in Namibia asked you to measure
the elevation of the crests of waves at Campus Point--without agreement
on some kind of standard, you wouldn't be able to do much more than
measure the heights of individual waves. If however, you could both
agree on an equivalent "sea level" at both localities, you could then
compare the absolute elevations of the wave crests.
U, and we always discuss or
measure differences relative to some arbitrary standard state.
Analogous to this might be if someone in Namibia asked you to measure
the elevation of the crests of waves at Campus Point--without agreement
on some kind of standard, you wouldn't be able to do much more than
measure the heights of individual waves. If however, you could both
agree on an equivalent "sea level" at both localities, you could then
compare the absolute elevations of the wave crests.

 , d
, d , and
, and 
 ?
?
 is used to indicate any kind of difference.
is used to indicate any kind of difference.
 is used to indicate a partial differential. For example, the partial differential, with respect to y, of
is used to indicate a partial differential. For example, the partial differential, with respect to y, of
 dQ
dQ
 indicates 'proportional') but if the
crystal is allowed to expand, some of the added energy will be consumed
by expansion dV, so the total energy of the crystal is reduced:
indicates 'proportional') but if the
crystal is allowed to expand, some of the added energy will be consumed
by expansion dV, so the total energy of the crystal is reduced:

 C = 0
C = 0
 2/
2/
 and
and  are the expansivity and compressibility--for solids the difference between CP and CV is minimal and can be ignored as a first approximation. For gases, CP = CV + R, and is quite significant.
are the expansivity and compressibility--for solids the difference between CP and CV is minimal and can be ignored as a first approximation. For gases, CP = CV + R, and is quite significant.

 CPdT
CPdT
 H produced by changing temperature by integrating the heat capacity CP:
H produced by changing temperature by integrating the heat capacity CP:
 H =
H =  CPdT
CPdT
 H):
H):
 H°298-1000 that results from heating quartz from 298 K to 1000 K, given the following heat capacity expansion coefficients:
H°298-1000 that results from heating quartz from 298 K to 1000 K, given the following heat capacity expansion coefficients:
 (CP dT =
(CP dT =  (a + bT + cT-2 + dT-0.5)
(a + bT + cT-2 + dT-0.5)
 HP=
HP= QP)
QP)
 H and heat change
H and heat change  Q is revealed by differentiating H = U + PV to obtain the total differential
Q is revealed by differentiating H = U + PV to obtain the total differential
 =
=  - V
- V 
 = 0, leaving
= 0, leaving
 =
= 
 =
=  = CP
= CP
 U with increasing temperature at constant pressure, we want to know
U with increasing temperature at constant pressure, we want to know  H, and we can get that by integrating the heat capacity CP over the temperature range of interest.
H, and we can get that by integrating the heat capacity CP over the temperature range of interest.
 H, though:
calorimetry. By dissolving a mineral in acid and measuring the heat
produced by the dissolution, we get a heat of dissolution (usually
positive). The enthalpy of "formation"
H, though:
calorimetry. By dissolving a mineral in acid and measuring the heat
produced by the dissolution, we get a heat of dissolution (usually
positive). The enthalpy of "formation"  fH°
of the mineral is then just the opposite of the heat of dissolution
(usually negative). Exceptions to the "usually positive/negative" rule
include CN, HCN, Cu2+, Hg2+, NO, Ag+, and S2-. Enthalpies of formation appear in tables of thermodynamic data and are usually referenced to 298 K and 1 atm.
fH°
of the mineral is then just the opposite of the heat of dissolution
(usually negative). Exceptions to the "usually positive/negative" rule
include CN, HCN, Cu2+, Hg2+, NO, Ag+, and S2-. Enthalpies of formation appear in tables of thermodynamic data and are usually referenced to 298 K and 1 atm.
 rH° we can measure the enthalpies of formation of the reactants and products
rH° we can measure the enthalpies of formation of the reactants and products  fH° and then take the difference between them as
fH° and then take the difference between them as
 rH° =
rH° =  fH°products-
fH°products-  fH°reactants
fH°reactants
 2H2O
2H2O
 fH° = -1434.11 kJ/mol
fH° = -1434.11 kJ/mol fH° = -285.830 kJ/mol
fH° = -285.830 kJ/mol 2H2O
2H2O fH° = -2022.63 kJ/mol
fH° = -2022.63 kJ/mol rH° =
rH° =  fH°gypsum -
fH°gypsum -  fH°anhydrite -
fH°anhydrite -  fH°water = -16.86 kJ/mol.
fH°water = -16.86 kJ/mol.
 rH° < 0 the reaction
produces a reduction in enthalpy and is exothermic (heat is given up by
the rock and gained by the surroundings). If
rH° < 0 the reaction
produces a reduction in enthalpy and is exothermic (heat is given up by
the rock and gained by the surroundings). If  rH°
> 0 the reaction produces an increase in enthalpy and is endothermic
(heat from the surroundings is consumed by the rock). An easy way to
remember this is that spontaneous reactions produce a decrease in
internal energy, and because we know that
rH°
> 0 the reaction produces an increase in enthalpy and is endothermic
(heat from the surroundings is consumed by the rock). An easy way to
remember this is that spontaneous reactions produce a decrease in
internal energy, and because we know that  HP
HP
 fH° at Temperatures Other Than 298 K
fH° at Temperatures Other Than 298 K
 rCP for the reaction that forms the mineral of interest:
rCP for the reaction that forms the mineral of interest:
 rCP =
rCP =  rCPproducts -
rCPproducts -  rCPreactants
rCPreactants
 fH° for quartz at 1000 K, we get coefficients for the heat capacities of Si, O2 and SiO2:
fH° for quartz at 1000 K, we get coefficients for the heat capacities of Si, O2 and SiO2:
 a = 24.254
a = 24.254
 b = 6.2225E-3
b = 6.2225E-3
 c = -3.5E5
c = -3.5E5
 d = -470.7
d = -470.7
 fH°1000 -
fH°1000 -  fH°298 =
fH°298 = 
 CP dT =
CP dT =  a*(1000-298) +
a*(1000-298) +  b/2*(10002-2982) -
b/2*(10002-2982) -  c*(1000-1-298-1) + 2
c*(1000-1-298-1) + 2 d*(10000.5-2980.5) = 5.511 kJ/mol
d*(10000.5-2980.5) = 5.511 kJ/mol
 fH°1000 = (
fH°1000 = ( fH°1000 -
fH°1000 -  fH°298) +
fH°298) +  fH°298 = 5.511 - 910.700 = -905.2 kJ/mol
fH°298 = 5.511 - 910.700 = -905.2 kJ/mol
 H°298-1000 that results from heating quartz from 298 K to 1000 K, which we calculated is 45.37 kJ/mol.
H°298-1000 that results from heating quartz from 298 K to 1000 K, which we calculated is 45.37 kJ/mol.


 >
> 

 >
> 

 dT
dT
 C = 0
C = 0


 , in this system is
, in this system is = NM
= NM
 Copyright c 2009 by C.H. Mak
Copyright c 2009 by C.H. Mak
 = N! / (Np1! * Np2! ...Npn!)
= N! / (Np1! * Np2! ...Npn!) is the probability that a given number of atoms n in a given number of sites N will have a particular configuration.
Or
is the probability that a given number of atoms n in a given number of sites N will have a particular configuration.
Or = ln N! -
= ln N! -  ln(Npi)!
ln(Npi)! = -N
= -N  pilnpi
pilnpi =
= 
 is the probability that a given number of atoms M in a given number of sites N will have a particular configuration.
is the probability that a given number of atoms M in a given number of sites N will have a particular configuration.  (This is engraved on Boltzmann's tomb in Vienna!)
(This is engraved on Boltzmann's tomb in Vienna!)

 rH and
rH and  rV, we can calculate entropies of reactions by using absolute entropies S and calculating a difference in entropy
rV, we can calculate entropies of reactions by using absolute entropies S and calculating a difference in entropy  rS. For example, if we know that
rS. For example, if we know that
 rS° = 106.7 - 41.42 - 31.80 - 2 * 205.138 = -376.8 J mol-1 K-1
rS° = 106.7 - 41.42 - 31.80 - 2 * 205.138 = -376.8 J mol-1 K-1
 -TS
-TS



 dP -
dP -  dT
dT
 = V
= V
 = -S
= -S

 G =
G =  H - T
H - T S
S
 fG° is
fG° is
 fG° =
fG° =  fH° - T
fH° - T fS°
fS°
 fH°CaSO4 = -1434.11 kJ/mole
fH°CaSO4 = -1434.11 kJ/mole
 fS° = S°CaSO4 - S°Ca - S°S - 2 * S°O2 = -376.796 J mol-1 K-1
fS° = S°CaSO4 - S°Ca - S°S - 2 * S°O2 = -376.796 J mol-1 K-1
 fG° =
fG° =  fH° - T
fH° - T fS° = -1434,110 - 298.15 * -376.796 = -1321.77 kJ/mol
fS° = -1434,110 - 298.15 * -376.796 = -1321.77 kJ/mol
 rG =
rG =  rH - T
rH - T rS
rS
 rH = T
rH = T rS
rS
 rG = 0
rG = 0
 H and
H and  S, and both of these are measurable or can be calculated.
S, and both of these are measurable or can be calculated.

 rG < 0, the Gibbs free energy
of the products is lower than the Gibbs free energy of the reactants
and the reaction moves to produce more products. If
rG < 0, the Gibbs free energy
of the products is lower than the Gibbs free energy of the reactants
and the reaction moves to produce more products. If  rG
> 0, the Gibbs free energy of the products is greater than the Gibbs
free energy of the reactants and the reaction moves to produce more
reactants.
rG
> 0, the Gibbs free energy of the products is greater than the Gibbs
free energy of the reactants and the reaction moves to produce more
reactants.  rG° at STP for the reaction
rG° at STP for the reaction
 rH° = 370 J
rH° = 370 J
 rS° = 3.7 J mol-1 K-1
rS° = 3.7 J mol-1 K-1
 rG° = 370 - 298.15 * 3.7 = -733 J/mol
rG° = 370 - 298.15 * 3.7 = -733 J/mol
 G tells us that calcite has lower Gibbs free energy and that the reaction runs forward (aragonite
G tells us that calcite has lower Gibbs free energy and that the reaction runs forward (aragonite  calcite).
calcite).
 rG =
rG =  VrdP -
VrdP -  SrdT
SrdT
 G = 0, such that
G = 0, such that
 rVdP =
rVdP =  rSdT
rSdT
 =
= 

 =
=  along an equilibrium,
along an equilibrium,  <
<  at high P and low T, and
at high P and low T, and  >
>  at high T and low P. Along the equilibrium boundary the Gibbs Free
energies of the reactants and products are equal and the Gibbs Free
energy of reaction
at high T and low P. Along the equilibrium boundary the Gibbs Free
energies of the reactants and products are equal and the Gibbs Free
energy of reaction  rG, is zero.
rG, is zero.
 H and
H and  S and Finding
S and Finding  G Directly
G Directly
 rG° =
rG° =  fG°products-
fG°products-  fG°reactants
fG°reactants
 fH° and
fH° and  fS°, it is often possible to obtain
fS°, it is often possible to obtain  fG°
values for most compounds from electronic data bases. For example, if
the following Gibbs free energies of formation are known:
fG°
values for most compounds from electronic data bases. For example, if
the following Gibbs free energies of formation are known:
 fG°CaSO4
fG°CaSO4 2H2O = -1707.280 kJ/mol
2H2O = -1707.280 kJ/mol
 fG°CaSO4 = -1321.790 kJ/mol
fG°CaSO4 = -1321.790 kJ/mol
 fG°H2O = -237.129 kJ/mol
fG°H2O = -237.129 kJ/mol
 2H2O
2H2O
 rG° = -1.232 kJ/mol
rG° = -1.232 kJ/mol
 rG at STP--but how do we calculate
rG at STP--but how do we calculate  rG
for other pressures and temperatures? Recall that the changes in Gibbs
free energy with pressure and temperature are given by two of Maxwell's
relations
rG
for other pressures and temperatures? Recall that the changes in Gibbs
free energy with pressure and temperature are given by two of Maxwell's
relations
 =
=  rV and
rV and  = -
= - rS
rS
 =
=  rV
rV P
P  = -
= - rS
rS T
T

 rGdP =
rGdP =
 rGP -
rGP -  rGPref =
rGPref =

 rVdP
rVdP  rGP =
rGP =  rGPref +
rGPref + 
 rVdP
rVdP

 rGdT =
rGdT =
 rGT -
rGT -  rGTref = -
rGTref = -

 rSdT
rSdT ΔrSdT
ΔrSdT rGPT =
rGPT =  rGPrefTref +
rGPrefTref + 
 rVdP -
rVdP - 
 rSdT
rSdT

 rVsdP =
rVsdP =  rVs(P - 1)
rVs(P - 1)

 rVsdP =
rVsdP =  rVsP
rVsP
 nepheline = 54.16 cm3
nepheline = 54.16 cm3
 albite = 100.43 cm3
albite = 100.43 cm3
 jadeite = 60.40 cm3
jadeite = 60.40 cm3
 rV and find
rV and find
 r
r =
=  nepheline +
nepheline +  albite - 2
albite - 2 jadeite = 33.79 cm3 = 3.379 J/bar
jadeite = 33.79 cm3 = 3.379 J/bar
 rGPT -
rGPT -  rG1,T =
rG1,T =  rVsP = 33.79 kJ/mol
rVsP = 33.79 kJ/mol
 rS depends on the heat capacity change of reaction
rS depends on the heat capacity change of reaction  rCP:
rCP:
 rS =
rS = 
 dT
dT
 rGT =
rGT =  rGTref -
rGTref - 
 rSdT
rSdT
 rGT =
rGT =  rGTref
-
rGTref
- 

 STref
+
STref
+ 
 dT
dT dT
dT
 a(T - T ln T)
-
a(T - T ln T)
-  bT2/2
-
bT2/2
-  cT-1/2 + 4
cT-1/2 + 4 dT0.5
-
dT0.5
-
 aTref
-
aTref
-  bTref2/2
+
bTref2/2
+  cTref-1
- 2
cTref-1
- 2 dTref0.5
+
dTref0.5
+
 aTlnTref
+
aTlnTref
+  bTTref
-
bTTref
-  cTTref-2/2
- 2
cTTref-2/2
- 2 dTTref-0.5
- T
dTTref-0.5
- T rSTref
+ Tref
rSTref
+ Tref rSTref
rSTref
 rG requires that you know
rG requires that you know  rG at the reference temperature.
rG at the reference temperature.
 rH at the reference temperature is
rH at the reference temperature is
 rGT =
rGT =
 rHTref
+
rHTref
+ 
 CPdT - T
CPdT - T
 rSTref
+
rSTref
+ 
 dT
dT
 rGP,T
rGP,T
 rH or
rH or  rG
rG
 rGP,T =
rGP,T =  rG1,Tref
-
rG1,Tref
- 

 rSTref
+
rSTref
+ 
 dT
dT dT
+
dT
+  rVsP
rVsP
 rGP,T =
rGP,T =
 rH1,Tref
+
rH1,Tref
+ 
 CPdT - T
CPdT - T
 rSTref
+
rSTref
+ 
 dT
dT +
+  rVsP
rVsP
 rGP,T =
rGP,T =  rG1,Tref
-
rG1,Tref
-  rS1,Tref(T - Tref)
+
rS1,Tref(T - Tref)
+  rVsP
rVsP
 rGP,T =
rGP,T =
 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
+
rS1,Tref
+  rVsP
rVsP
 rG for jadeite + quartz = albite at 800 K and 20 kbar. The data at 298 K and 1 bar are
rG for jadeite + quartz = albite at 800 K and 20 kbar. The data at 298 K and 1 bar are
 rH° = 15.86 kJ/mol
rH° = 15.86 kJ/mol
 rS° = 51.47 J K-1 mol-1
rS° = 51.47 J K-1 mol-1
 rVs° = 1.7342 J/bar = 17.342 cm3/mol
rVs° = 1.7342 J/bar = 17.342 cm3/mol
 rGP,T =
rGP,T =
 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
+
rS1,Tref
+  rVsP
rVsP
 rG = 0 at equilibrium, then we can write our solids-only and constant-heat-capacity approximations as
rG = 0 at equilibrium, then we can write our solids-only and constant-heat-capacity approximations as
 rG1,T
-
rG1,T
-  rS1,Tref(T - Tref)
+
rS1,Tref(T - Tref)
+  rVsP
rVsP
 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
+
rS1,Tref
+  rVsP
rVsP

 rG1,Tref
-
rG1,Tref
-  rS1,Tref(T - Tref)
rS1,Tref(T - Tref) / -
/ - rVs
rVs

 rH1,Tref
- T
rH1,Tref
- T rS1,Tref
rS1,Tref / -
/ - rVs
rVs

 rG1,Tref +
rG1,Tref +  rVsP
rVsP /
/  rS1,Tref
rS1,Tref

 rH1,Tref
+
rH1,Tref
+  rVsP
rVsP /
/  rS1,Tref
rS1,Tref


 dnfayalite +
dnfayalite +  dnforsterite
dnforsterite

 A and
A and  B.
B.
 i
i
 A and
A and  B?
Graphically, the partial molar volumes are the A and B axis intercepts
of the tangent to the mixing curve, and can be described by the simple
relationship:
B?
Graphically, the partial molar volumes are the A and B axis intercepts
of the tangent to the mixing curve, and can be described by the simple
relationship:
 A + XB
A + XB B
B  Xi
Xi i
i
 A = (Vmix - XB
A = (Vmix - XB B) / XA
B) / XA
 Smix = -R
Smix = -R  (Xi ln Xi)
(Xi ln Xi)
 Hmix = 0.5 * N z XAXB [2
Hmix = 0.5 * N z XAXB [2 AB -
AB -  AA -
AA -  BB]
BB]
 AB is the interaction energy among A-B atoms,
AB is the interaction energy among A-B atoms,  AA is the interaction energy among A-A atoms, and
AA is the interaction energy among A-A atoms, and  BB is the interaction energy among B-B atoms.
BB is the interaction energy among B-B atoms.

 μ, μ - μ°, or μ - G°.
μ, μ - μ°, or μ - G°.
 A - G°A =
A - G°A =  A -
A -  °A = RT lnXA
°A = RT lnXA B - G°B =
B - G°B =  B -
B -  °B = RT lnXB
°B = RT lnXB

 μ
= 0, and when the mineral is infinitely dilute (X = 0), the chemical
potential is undefined. For example, in a two-component mineral if XA = 0.4, at T = 298 K,
μ
= 0, and when the mineral is infinitely dilute (X = 0), the chemical
potential is undefined. For example, in a two-component mineral if XA = 0.4, at T = 298 K,
 Gmix line is the sum of the chemical potentials of the endmembers:
Gmix line is the sum of the chemical potentials of the endmembers:
 Gmix = RT (XA ln XA + XB ln XB) or
Gmix = RT (XA ln XA + XB ln XB) or
 Gmix = RT
Gmix = RT  (Xi ln Xi)
(Xi ln Xi)

 Hmix = 0. If this is not true,
Hmix = 0. If this is not true,  Gmix is not a simple function of composition, but has the general form:
Gmix is not a simple function of composition, but has the general form:

 Hmix and -T
Hmix and -T Smix,
the free energy of mixing may be negative throughout the whole
composition range if the entropic energy contribution outweighs the
enthalpy increase; this is more likely at higher temperature.
Smix,
the free energy of mixing may be negative throughout the whole
composition range if the entropic energy contribution outweighs the
enthalpy increase; this is more likely at higher temperature.
 Hmix > 0, i.e., if 2
Hmix > 0, i.e., if 2 AB >
AB >  AA +
AA +  BB,
which makes sense because it means that the A-B bonds have a higher
free energy than the sum of the free energies of separate AA and BB
bonds.
BB,
which makes sense because it means that the A-B bonds have a higher
free energy than the sum of the free energies of separate AA and BB
bonds.
 X)
X)
 is the "site occupancy coefficient" (e.g.,
is the "site occupancy coefficient" (e.g.,  = 2 for Mg in Mg2SiO4), and
= 2 for Mg in Mg2SiO4), and  is the activity coefficient that describes the non-ideal behavior. Thus we write
is the activity coefficient that describes the non-ideal behavior. Thus we write
 =1.
As a specific example, the chemical potential of the almandine (Fe3Al2Si3O12) component of a garnet solid solution ((Fe, Mg, Ca, Mn)3Al2Si3O12) is
=1.
As a specific example, the chemical potential of the almandine (Fe3Al2Si3O12) component of a garnet solid solution ((Fe, Mg, Ca, Mn)3Al2Si3O12) is
 rμ = 0 = cμC + dμD - aμA - bμB
rμ = 0 = cμC + dμD - aμA - bμB
 rμ =
rμ = 
 i μi
i μi
 i is the
stochiometric coefficient of a product or reactant and is positive if
for a product and negative if for a reactant. If we then remember that
i is the
stochiometric coefficient of a product or reactant and is positive if
for a product and negative if for a reactant. If we then remember that  rμ = 0 = c(μC° + RT lnaC) + d(μD° + RT lnaD) - a(μA° + RT lnaA) - b(μB° + RT lnaB)
rμ = 0 = c(μC° + RT lnaC) + d(μD° + RT lnaD) - a(μA° + RT lnaA) - b(μB° + RT lnaB)
 rμ =
rμ =  rμ° + RT ln (aCc aDd/aAa aBb)
rμ° + RT ln (aCc aDd/aAa aBb)
 rμ =
rμ =  rμ° + RT ln
rμ° + RT ln  ai
ai (
( means to multiply all i terms)
means to multiply all i terms)
 rμ =
rμ =  rμ° + RT lnQ
rμ° + RT lnQ
 rμ°
is the difference in the Gibbs free energies of the products and
reactants when each is in its pure reference state and varies as a
function of pressure and temperature.
rμ°
is the difference in the Gibbs free energies of the products and
reactants when each is in its pure reference state and varies as a
function of pressure and temperature.  rμ is the difference in the Gibbs free energies of the products and reactants as they actually occur and varies as a function of phase composition.
rμ is the difference in the Gibbs free energies of the products and reactants as they actually occur and varies as a function of phase composition.
 rμ = 0. We write this (with K instead of Q, to signify equilibrium) as
rμ = 0. We write this (with K instead of Q, to signify equilibrium) as
 rG° = -RT ln K
rG° = -RT ln K
 rG° = -20.12 kJ/mol
rG° = -20.12 kJ/mol
 rG° = -RT lnK
rG° = -RT lnK



 iMi
iMi
 i are the stoichiometric coefficients and Mi are the masses or the phase components. Analogously, we can explicitly write a similar balance among the chemical potentials:
i are the stoichiometric coefficients and Mi are the masses or the phase components. Analogously, we can explicitly write a similar balance among the chemical potentials:

 iμi
iμi

 iμ°i +
iμ°i + 
 iRTln ai
iRTln ai

 iμ°i +
iμ°i +  RTln (ai)
RTln (ai)

 iμ°i + RTln
iμ°i + RTln  ai
ai

 iμ°i + RTln K
iμ°i + RTln K
 rG° + RT ln K
rG° + RT ln K
 rG° = -RT ln K
rG° = -RT ln K
 ai
ai
 rH° - T
rH° - T rS° = - RT ln K
rS° = - RT ln K
 rH1,Tref
+
rH1,Tref
+ 
 CPdT - T
CPdT - T
 rSTref
+
rSTref
+ 
 dT
dT +
+ 
 rVP = - RT ln K
rVP = - RT ln K
 rG° / RT) = [(
rG° / RT) = [( rH / RT) - (
rH / RT) - ( rS / R)]
rS / R)]

 Smix = -R
Smix = -R  Xi ln Xi
Xi ln Xi
 Al2Si3O12, the activities are
Al2Si3O12, the activities are
 Mg3XMg3
Mg3XMg3
 Fe3XFe3
Fe3XFe3
 Ca3XCa3
Ca3XCa3
 Mn3XMn3
Mn3XMn3

 ions,
ions,

 power. For non-ideal mixing, we include an activity coefficient
power. For non-ideal mixing, we include an activity coefficient 
 j
j Xj
Xj
 (Y,Z)
(Y,Z)
 Y
Y , A
, A Z
Z , B
, B Y
Y , and B
, and B Z
Z .
.
 Y
Y = XA
= XA XY
XY
 Z
Z = XA
= XA XZ
XZ
 Y
Y = XB
= XB XY
XY
 Z
Z = XB
= XB XZ
XZ
 Mg3 XMg3
Mg3 XMg3
 Al2 XAl2
Al2 XAl2
 Fe3 XFe3
Fe3 XFe3
 Al2 XAl2
Al2 XAl2
 Ca3 XCa3
Ca3 XCa3
 Al2 XAl2
Al2 XAl2
 Mn3 XMn3
Mn3 XMn3
 Al2 XAl2
Al2 XAl2
 Ca3 XMn3
Ca3 XMn3
 Fe3+2 XFe3+2
Fe3+2 XFe3+2

 3 and Al from 0
3 and Al from 0  2.
2.
 rV is small, such that
rV is small, such that
 =
= 
 rG = -RT ln (aprpaann)/(aalmaphl)
rG = -RT ln (aprpaann)/(aalmaphl)
 = 1) in garnet and biotite and assume that there is mixing on only 1 site
= 1) in garnet and biotite and assume that there is mixing on only 1 site

 rG° / RT) = -(
rG° / RT) = -( rH / RT) - (P
rH / RT) - (P rV / RT) + (
rV / RT) + ( rS / R)
rS / R)
 rS = 3*0.782*R = 19.51 J/mol K
rS = 3*0.782*R = 19.51 J/mol K
 rH / R) - (P
rH / R) - (P rV / R) = -2109
rV / R) = -2109
 rH = 3*2109*R -2070*
rH = 3*2109*R -2070* rV
rV
 rV = 0.238 J/bar, thus
rV = 0.238 J/bar, thus
 rH = 52.11 kJ/mol
rH = 52.11 kJ/mol

 rV is large and relatively insensitive to temperature. A popular one is GASP:
rV is large and relatively insensitive to temperature. A popular one is GASP:

 rG
= -RT ln [(aqtzaky2agrs) / aan3]
= -RT ln agrs / aan3
rG
= -RT ln [(aqtzaky2agrs) / aan3]
= -RT ln agrs / aan3
 rV = -6.608 J/bar. Again, if we use
rV = -6.608 J/bar. Again, if we use
 rH / RT) - (P
rH / RT) - (P rV / RT) + (
rV / RT) + ( rS / R)
rS / R)
 rV / R) = -(
rV / R) = -( rH / R) + (T
rH / R) + (T rS / R)
rS / R)
 rS /
rS /  rV -
rV -  rH /
rH /  rV
rV
 rS /
rS /  rV = 22.8 then
rV = 22.8 then  rS = -150.66 J/mol K
rS = -150.66 J/mol K
 rH /
rH /  rV = 7317 then
rV = 7317 then  rH = -48.357 kJ/mol
rH = -48.357 kJ/mol


 G*.
G*.
 G*;
iii) temperature dependence of transformation. We can draw a similar
diagram for a change in enthalpy induced by the reaction
G*;
iii) temperature dependence of transformation. We can draw a similar
diagram for a change in enthalpy induced by the reaction  rH and an activation enthalpy barrier
rH and an activation enthalpy barrier  H* (usually called an activation energy Q*). Of course, unlike
H* (usually called an activation energy Q*). Of course, unlike  rG,
rG,  rH can be positive or negative:
rH can be positive or negative:

 S*, however, in general, reactions with positive entropy change
S*, however, in general, reactions with positive entropy change  rS
are faster. For example, evaporation is faster than condensation,
melting is faster than crystallization, and disordering is faster than
ordering.
rS
are faster. For example, evaporation is faster than condensation,
melting is faster than crystallization, and disordering is faster than
ordering.  H* is
H* is
 H*/RT)
H*/RT)

 ;
ii) fraction of atoms with thermal energy greater than Q*; and iii)
probability p that the atom jumping satisfies some geometrical
consideration (this is a fancy name for a fudge factor):
;
ii) fraction of atoms with thermal energy greater than Q*; and iii)
probability p that the atom jumping satisfies some geometrical
consideration (this is a fancy name for a fudge factor):
 p
p  exp(-Q*/RT)
exp(-Q*/RT)
 (kT/h)
(kT/h)  exp(-Q*/RT)
exp(-Q*/RT)
 at which atoms jump is related to temperature and to atom-scale processes described by k and h.
at which atoms jump is related to temperature and to atom-scale processes described by k and h.
 VG, the Gibbs free energy change of reaction per unit volume. Nucleation is opposed by an interfacial energy
VG, the Gibbs free energy change of reaction per unit volume. Nucleation is opposed by an interfacial energy  and a strain energy
and a strain energy  . The overall change in nucleation energy for a spherical nucleus of radius r is then
. The overall change in nucleation energy for a spherical nucleus of radius r is then
 nG =
nG =  VG +
VG +  Ginterfacial +
Ginterfacial +  Gstrain = (4/3)
Gstrain = (4/3) r3
r3 VG + 4
VG + 4  r2
r2 + (4/3)
+ (4/3) r3
r3

 / (
/ ( VG +
VG +  )
)
 nG =
nG =  G*, the activation energy for nucleation is
G*, the activation energy for nucleation is
 G* = 16
G* = 16 
 3 / 3(
3 / 3( VG +
VG +  )2
)2
 is:
is:
 =
=  (kT/h) exp( -Q*/RT)[( -
(kT/h) exp( -Q*/RT)[( - rG/RT)]
rG/RT)]
 is an "interface jump distance" and the rest you will recognize from previous equations. The [( -
is an "interface jump distance" and the rest you will recognize from previous equations. The [( - rG/RT)] term indicates that the rate of growth depends on the Gibbs free energy change of reaction. As
rG/RT)] term indicates that the rate of growth depends on the Gibbs free energy change of reaction. As  rG
rG  0, this term also approaches zero. As
0, this term also approaches zero. As  rG
rG 
 , this term approaches 1.
, this term approaches 1.
 = 1 - exp[(4/3)
= 1 - exp[(4/3)


 dt]
dt]
 = 1 - exp{(6.7/d)
= 1 - exp{(6.7/d) [1-exp(
[1-exp(

 [
[ 2(t -
2(t -  )2 - y2] d
)2 - y2] d )] dy}
)] dy}
 = 1 - exp(-ktn)
= 1 - exp(-ktn)

 )
)
 )
)
 )]
)]
 )]
)]
 H, S, V, CP) of zeolites have been measured, and we can use those properties to calculate a phase diagram for the CASH system:
H, S, V, CP) of zeolites have been measured, and we can use those properties to calculate a phase diagram for the CASH system: